BEM - velocity triangle video
1 Test description
This test checks that the output from the
BEM algorithm
is correct by comparing the results from Ashes to hand-calculated ones. The load case used for the calculation is the one from the
Velocity Triangle video
, which features the
NREL 5-MW reference wind turbine
in near rated condition
The following load cases are tested
- Steady BEM
- Unsteady BEM
- Steady BEM - Flexible blades
- Unsteady BEM - Flexible blades
2 Model
This test uses the
RNA only
template
The CSV file to run this test can be downloaded from
here
.
The model used for this test is shown in the figure below:

For this test, we focus on the
Blade aerodynamical station
number 7 of blade 1. This blade station has a chordlength
$$c=4.458\text{ m}$$
and a twist angle
$$\theta = 10.162\text{ deg}$$
.The distance from the blade station to the blade root is
$$r=18.45\text{ m}$$
.
Note
: in the video, the Blade station number is 6. This is because the naming has changed between when the video was made and now (the innermost station use to be called 0, it is now called 1)
The radius if the hub of the RNA is
$$r_h=1.5\text{ m}$$
This blade station uses the
NREL 5-MW DU 99-W-350
airfoil, which polars are shown below:
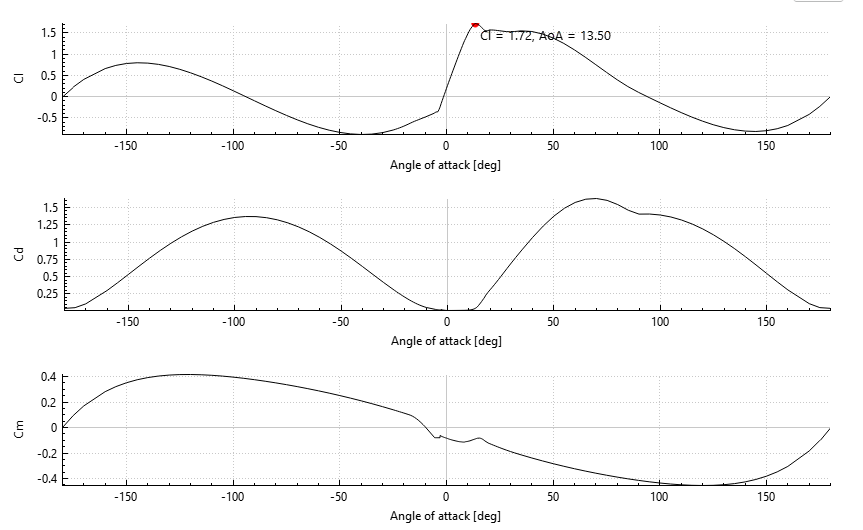
The air density is
. Tip and hub corrections are set to 0.
For the analytical solution, the RPM is set to the RPM at which the simulation stabilises in Ashes, which is 11.74 RPM. The wind velocity is set to 10 ms.
The kinematic viscosity is
$$\nu=1.478\cdot10^{-5}\text{ m}^2\cdot\text{s}^{-1}$$
and the speed of sound is
$$c_s = 343\text{ m}\cdot\text{s}^{-1}$$
3 Analytical solution
The wind speed and rotational speed are denoted
$$V$$
and
$$\omega$$
, respectively.
In order to compute the aerodynamic loads, we need to find the lift and drag coefficients for a given blade station. We do this using the steady BEM algorithm defined by
Hansen (2008d)
and summed up below:
-
define initial axial and tangential induced velocities as
$$a = 0.33$$and$$a_t = 0$$, respectively
-
the flow angle is defined as
$$\phi = \tan^{-1}\frac{(1-a)\cdot V}{(1+a_t)\cdot\omega\cdot(r+r_h)}$$
-
the angle of attack is obtained by substracting the twist
$$\theta$$and the pitch$$\gamma$$to the flow angle. The angle of attack is thus$$\alpha = \phi-\theta-\gamma$$
-
the lift and drag coefficients
$$C_L$$and$$C_D$$are then looked up from the polars. Linear interpolation is used if the current angle of attack is not in the look-up table.
-
the blade solidity is calculated as
$$\sigma = \frac{cB}{2\pi(r+r_h)}$$, where$$B = 1$$is the number of blades
-
new values for the induced velocities are computed as
$$a = \frac{1}{\frac{4\sin^2\phi}{\sigma C_n}+1}$$and
$$a_t = \frac{1}{\frac{4\sin\phi\cos\phi}{\sigma C_t}+1}$$
where$$C_n = C_L\cos\phi+C_D\sin\phi$$and$$C_t = C_L\sin\phi - C_D\cos\phi$$ - compare the induced velocities to the previous values. If the difference is larger than 0.001, repeat steps 2 to 6
-
the relative velocity is defined as
$$V_{rel}=\sqrt{((1-a)\cdot V)^2+((1+a_t)\cdot\omega\cdot(r+r_h))^2}$$
-
the lift and drag forces are then
$$F_{D} = \frac{1}{2}\rho cC_DV_{rel}^2$$and
$$F_{L} = \frac{1}{2}\rho cC_LV_{rel}^2$$
-
The pitching moment is then
$$M_P=\frac{1}{2}\rho c^2C_MV_{rel}^2$$
-
the thust and torque forces are then
$$F_{th} = F_{L}\cos\phi+F_{D}\sin\phi$$and
$$F_{t} = -F_{D}\cos\phi + F_{L}\sin\phi$$
More details on the theory and the equations can be found in the
BEM algorithm
section.
The following results can be derived from the algorithm:
-
The angle of attack is
$$\alpha = 6.38\text{ deg}$$
-
The lift, drag and moment coefficients are
$$C_l = 1.055, C_d=0.01123, C_m = -0.1116$$
-
The axial induction factor is
$$a=0.2504$$
-
The tangential induction factor is
$$a_t=0.02914$$
-
The relative velocity is
$$V_{rel}=\sqrt{((1-a)V)^2+((1+at)wr)^2}=26.33\text{ m}\cdot\text{s}^{-1}$$
-
The Reynolds number is
$$Re=Vrel\cdot c/\nu=7.94\cdot10^6$$
-
The Mach number is
$$Ma = V_{rel}/C_s=0.0768$$
-
The lift and drag forces are
$$F_L=1998\text{ N}\cdot\text{m}^{-1}, F_D=21.25\text{ N}\cdot\text{m}^{-1}$$
-
The pitching moment is
$$M_P = -941.7\text{ Nm}\cdot\text{m}^{-1}$$
-
The thrust and torque forces are
$$F_{th}=1921\text{ N}\cdot\text{m}^{-1}, F_t=548.4\text{ N}\cdot\text{m}^{-1}$$
Note:
The conditions are steady once the rotor reaches a constant RPM, so it is expected that the unsteady BEM and the steady BEM will give very similar results.
The flexible blades are modelled as having a very high stiffness, so even though they are called 'flexible' it is expected that they will produce very similar results. The reason we do this is because it is possile to model the blades as infinitely stiff (in which case they do not have structural properties) or as flexible (with a user-defined stiffness, in the current case very high). By having these two cases, we check that both ways of modelling the blades produce the correct results.
The flexible blades are modelled as having a very high stiffness, so even though they are called 'flexible' it is expected that they will produce very similar results. The reason we do this is because it is possile to model the blades as infinitely stiff (in which case they do not have structural properties) or as flexible (with a user-defined stiffness, in the current case very high). By having these two cases, we check that both ways of modelling the blades produce the correct results.
4 Results
A simulation of 90 seconds is run. The test is considered passed if the last 20% of the results produced by Ashes lie within 0.5% of the analytical solution.
The report with the results can be found here: