Eigenfrequency circular cylinder
1 Test description
This test uses a cantilever beam model woth a constant circular hollow cross section fixed into the ground. The eigenfrequency of the model computed by Ashes is benchmarked against the analyrical solution.
2 Model
This test uses the
Tubular tower only
template.
The csv file to run this test can be downloaded from
here
.
The model is shown in the figure below:

The model has a homogeneous circular hollow cross section of diameter
$$D = 6\text{ m}$$
and thickness
$$t=0.06\text{ m}$$
. The length of the beam is
$$l = 30\text{ m}$$
.
The material is steel, with an Elastic modulus
$$E = 2.1\cdot10^{11}\text{ Pa}$$
and a density
$$d=7850\text{ kg}\cdot{m}^{-3}$$
.
The number of elements into which the structure is divided is a crucial parameter for matching the analytical solution and is studied in section 4.
Note:
this structure has the same characteristics as the Monopile for the OC3 model with a rigid foundation. However, it will not have the same eigenfrequencies as the
Monopile only
model in Ashes (even though that is the monopile of the OC3 model) since that model is partly submerged. Therefore, the added mass will influence the eigenfrequencies.
3 Analytical solution
The cross sectional area is thus
$$A=\pi(D/2)^2-\pi(D/2-t)^2=1.120\text{ m}^2$$
which gives a distributed mass
$$m = A\cdot d = 8789\text{ kg}\cdot{m}^{-1}$$
and the second moment of area is
$$I=\pi/4\left[(D/2)^4-(D/2-t)^4\right]=4.939\text{ m}^4$$
.
Under this configuration, the analytical solution for the first eigenfrequency of the structure is
$$f_1=\frac{\beta_1^2}{2\pi}\cdot\sqrt{\frac{EI}{m}}=6.754\text{ Hz}$$
with
$$\beta_1l=0.596864\pi$$

4 Convergence study
Since structures in Ashes are modelled using the finite element method, how well the eigenfrequency of the struture will match the analytical solution depends on the number of elements used.
The graph below shows the 1st eigenfrequency computed by Ashes against the number of elements used for the discretisation. The solid red line shows the analytical solution and the dotted line shows 99.9% of the analytical solution.
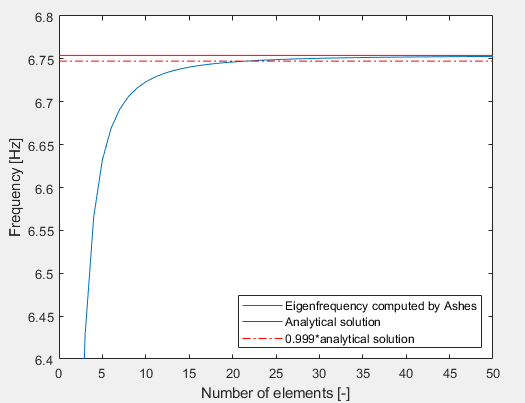
The data in this graph shows that 22 elements are necessary to be within 0.1% of the analytical solution. This nuber of elements is chosen for this test.
Note
: the same analysis shows that 68 elements were needed for be within 0.01% of the analytical solution. This is not shown in the graph.
5 Results
The test is considered passed if the eigenfrequency computed by Ashes lies within 0.1% of the analytical solution.
Once the test is live, the report for this test can be found on the following link: