IEC extreme events
The extreme wind events used in the Design Load Cases suggested by
IEC-61400-1 (2019)
(see
DLC - Design Load Case
) are available in Ashes in the
IEC extreme wind
part. This section summarizes the equations used to model these extreme events.
1 General
Two parameters are used in several extreme wind models:
-
The longitudinal turbulence scale parameter
$$\Lambda_1$$, in meters, is defined as
$$\Lambda_1=\left\{\begin{array}{ll}0.7z&\text{for }z\leq 60 \text{ m}\\ 42&\text{for }z>60 \text{ m}\end{array}\right.$$
-
The representative value of the turbulence standard deviation
$$\sigma_1$$, in$$\text{m}\cdot\text{s}^{-1}$$, is defined as
$$\sigma_1 = I_{ref}(0.75V_{hub}+5.6)$$where$$I_{ref}$$is a reference value of the turbulence intensity. Note that this value depends on the turbulence category. -
Currently, this value is hardcoded to 0.16, corresponding to a turbulence category A
In addition, the extreme wind speed with return periods of 50 and 1 year, respectively
$$V_{e50}(z)$$
and
$$V_{e1}(z)$$
are defined as
$$V_{e50}(z)=1.4\cdot V_{ref}\left(\frac{z}{z_{hub}}\right)^{0.11}$$
$$V_{e1}(z)=0.8\cdot V_{e50}(z)$$
where
-
$$V_{ref}$$is the reference wind speed, input by the user
-
$$z_{hub}$$is the hub height
2 Extreme coherent gust with direction change (ECD)
3 Extreme direction change (EDC)
For this extreme wind, the wind magnitude does not change but the wind angle
$$\theta(t)$$
will vary from its initial value
$$\theta_0$$
(defined by the user) to
$$\theta_0+\theta_e$$
, with
$$\theta_e=4\arctan{\left[\frac{\sigma_1}{V_{hub}\left(1+0.1(D/\Lambda_1)\right)}\right]}$$
Note:
the extreme direction change depends on the wind velocity
The variation of the wind angle is then given by
$$\theta(t)=\large{\left\{\begin{array}{ll}\theta_0&\text{for }0\leq t< T_{start}\\ \theta_0+0.5\cdot\theta_e\left(1-\cos{(\pi\cdot t/T)}\right)&\text{for }T_{start}\leq t\leq T_{start} + T\\ \theta_e&\text{for }t>T_{start}+T\end{array}\right.}$$
with
-
$$T_{start}$$the start of the extreme wind event
-
$$T$$the duration of the event, given in IEC-61400-1 (2019) as$$T = 6\text{ s}$$
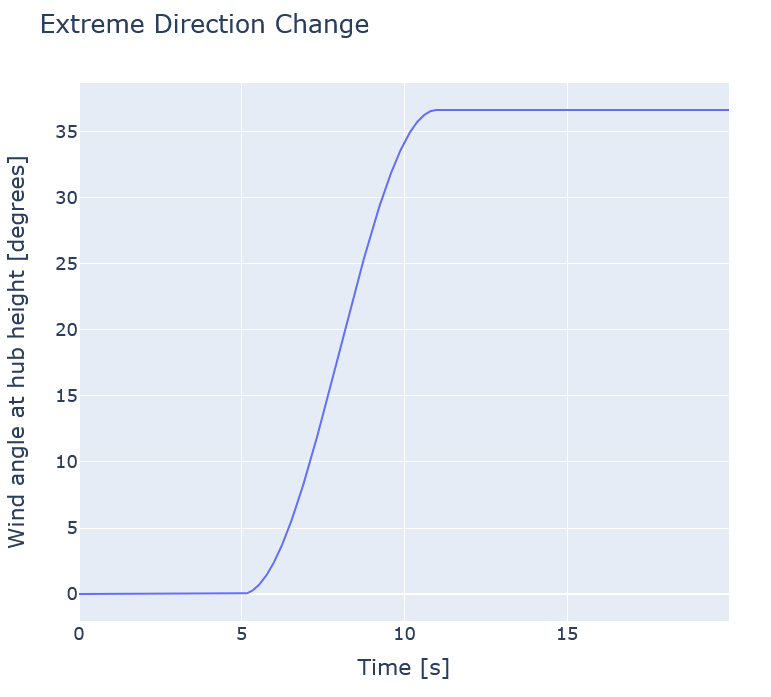
The figure below illustrates the Extreme Direction Change for
$$T_{start} = 10\text{ s}$$
and
$$V_{hub} = 10\text{ m}\cdot\text{s}^{-1}$$
4 Extreme operating gust (EOG)
Often referred to as
Mexican hat
. For this model, we define the gust magnitude at hub height
$$V_{gust}$$
as
$$V_{gust}=\text{min}\left\{1.35\left(V_{e1}-V_{hub}\right);3.3\frac{\sigma_1}{1+0.1(D/\Lambda_1)}\right\}$$
where
-
$$V_{e1}$$,$$\sigma_1$$and$$\lambda_1$$are defined in section 1
-
$$V_{hub}$$is the average wind speed at the hub height, correponding to the Initial wind speed parameter in Ashes
-
$$D$$is the projected diameter of the rotor
The wind speed at height
$$z$$
is then defined by
$$V(t,y,z)=\large{\left\{\begin{array}{ll}V_{hub}\left(\frac{z}{z_{hub}}\right)^\alpha - 0.37V_{gust}\sin\left(3\pi t/T\right)\left(1-\cos\left(2\pi t/T\right)\right)&\text{for }0\leq t\leq T\\ V_{hub}\left(\frac{z}{z_{hub}}\right)^\alpha&\text{for }t>T\end{array}\right.}$$
with
-
$$\alpha = 0.2$$the power law exponent (as defined in Wind profile power law )
-
$$T$$the duration of the extreme event, given in IEC-61400-1 (2019) as$$T = 10.5\text{ s}$$
5 Extreme wind model (EWM)
The Extreme wind model can be chosen to be
Steady
or
Turbulent
. The EWM uses a reference wind speed
$$V_{ref}$$
as an input. This parameter is defined by the wind turbine class.
5.1 Steady EWM
For the steady exreme wind model, the 50-year return period extreme wind is computed as
$$V_{e50}=1.4V_{ref}\left(\frac{z}{z_{hub}}\right)^{0.11}$$
The 1-year return period extreme wind is computed as
$$V_{e1}=1.12V_{ref}\left(\frac{z}{z_{hub}}\right)^{0.11}$$
5.2 Turbulent EWM
For the turbulent extreme wind model, the 50-year return period 10-minute average wind speed is computed as
$$V_{e50} = V_{ref}\left(\frac{z}{z_{hub}}\right)$$
The 1-year return period 10-minute average wind speed is computed as
$$E_{e1}=0.8V_{ref}\left(\frac{z}{z_{hub}}\right)$$
The longitudinal turbulence standard deviation is given as
$$\sigma_1 = 0.11V_{hub}$$
Note
: only the
Steady EWM
is is implemented in the
IEC extreme wind
part. However, the
Turbulent EWM
can easily be modeled using the
Turbulent Wind Creator
or with the
Batch manager
.
6 Extreme wind shear (EWS)
The extreme wind shear can be applied horizontally (
EWSV
) or vertically (
EWSH
). This is done by adding a wind speed transient to the wind distribution calculated with the
Wind profile power law
.
The vertical extreme wind shear is defined by
$$V(t,z)=\large{\left\{\begin{array}{ll}V_{hub}\left(\frac{z}{z_{hub}}\right)^{\alpha}\pm \left(\frac{z-z_{hub}}{D}\right)\left[2.5+0.2\beta\sigma_1\left(\frac{D}{\Lambda_1}\right)^{0.25}\right]\left(1-cos(2\pi t/T)\right)&\text{for }0\leq t\leq T\\ V_{hub}\left(\frac{z}{z_{hub}}\right)^\alpha&\text{for }t>T\end{array}\right.}$$
and the horizontal extreme wind shear is defined by
$$V(t,y,z)=\large{\left\{\begin{array}{ll}V_{hub}\left(\frac{z}{z_{hub}}\right)^\alpha \pm \left(\frac{y}{D}\right)\left[2.5+0.2\beta\sigma_1\left(\frac{D}{\Lambda_1}\right)^{0.25}\right]\left(1-cos(2\pi t/T)\right)&\text{for }0\leq t\leq T\\ V_{hub}\left(\frac{z}{z_{hub}}\right)^\alpha&\text{for }t>T\end{array}\right.}$$
with
-
$$\alpha = 0.2$$the power law exponent (as defined in Wind profile power law )
-
$$\beta = 6.4$$
-
$$T = 12$$s the time during which the extreme shear is applied
-
$$\Lambda_1$$the turbulence scale parameter, as defined in Equation 1
-
$$\sigma_1$$the turbulence standard deviation, as defined in Equation 2
-
$$D$$is the projected rotor diameter
Ashes offers the possibilty to start the extreme event after a given time, defined by the
Start of extreme wind event
parameter in the
IEC extreme wind
part, noted
$$t_{start}$$
. In this case, the temporal coordinate
$$t$$
will be replaced by
$$t-t_{start}$$
.
The sign of the wind speed transient (the
$$\pm$$
sign in the equations above), for both vertical and horizontal shear, is set by the user with the
Sign
parameter in the
IEC extreme wind
part