Fatigue analysis procedure
Ashes can compute an estimation of the
fatigue life
for a
Fatigue sensor
. The file output from the sensor will produce fatigue lives for each stress point defined by the user.
For each stress point, two fatigue lives are computed: a fatigue life
from histogram
and a fatigue life
from range
.
This document explains the procedure of obtaining both fatigue life estimates. Here we assume that the fatigue analysis parameters have been defined (either in the
Preferences
window or in the
Support section files
).
The process runs as follows:
1 Fatigue life directly from ranges
During a time simulation, if a fatigue sensor has been added to a beam element or to a joint, a fatigue life estimation will be computed at each time step. This is performed as follows.
1.1 Compute the stress time history
During a time simulation, the stresses on the
stress points
will be computed depending on the
SCFs
defined by the user or pre-computed by Ashes.
1.2 Perform a Rainflow counting
The
Rainflow counting algorithm
implemented in Ashes will produce a series of stress ranges, corresponding to the ampitude of the cycles found during the time simulation. Each new stress range means that a new cycle has been counted by the Rainflow counting algorithm.
Note that cycles are counted
live
, which means that during the time simulation, the variations in stress will add new cycles to the existing series of stress ranges.
The figures below illustrate this procedure. In the first case, a sinusoidal stress of amplitude
$$A_1 = 105.5\text{ MPa}$$
and period
$$T_1 = 10\text{ s}$$
is applied (blue curve).
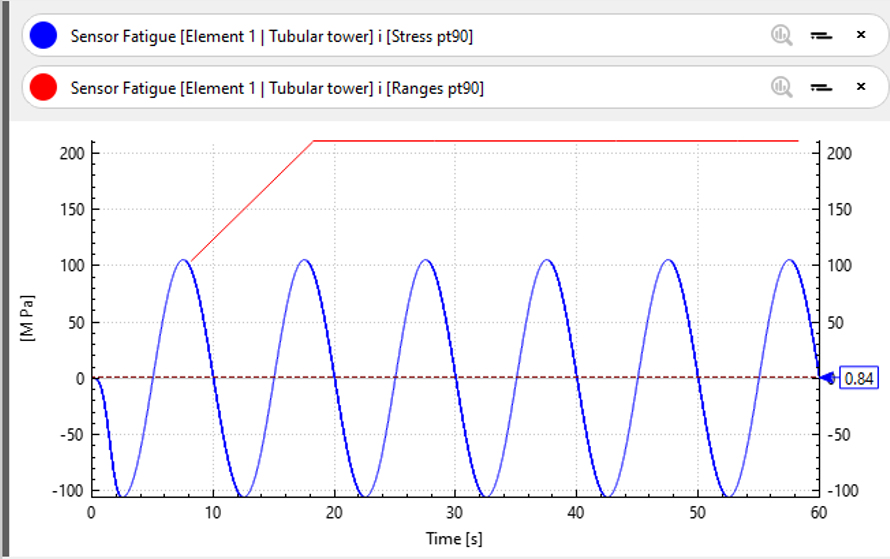
After 60 seconds, the Ranflow counting algorithm will have counted one cycle of range
$$A_1$$
and 5 cycles of range
$$2A_1$$
. The stress ranges are plotted in the red curve, however note that this is not a time series but rather a
counting
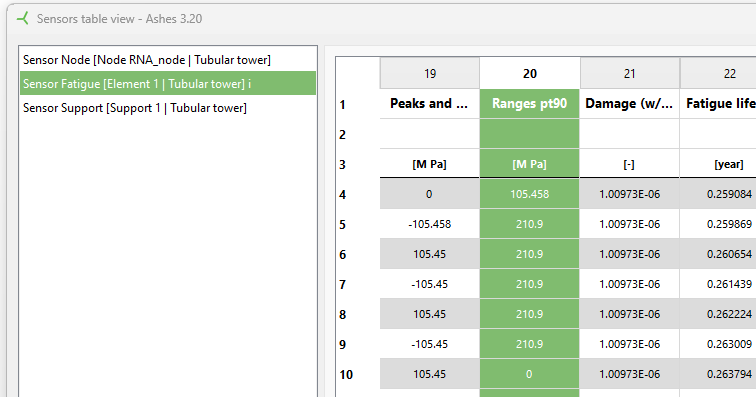
of cycles, as shown in the table below
In the second case, the stress changes after 30 seconds to a sinusoidal stress of ampltude
$$A_2=A_1/2=52.75\text{ MPa}$$
and a period
$$T_2=T_1/2=5\text{ s}$$
.
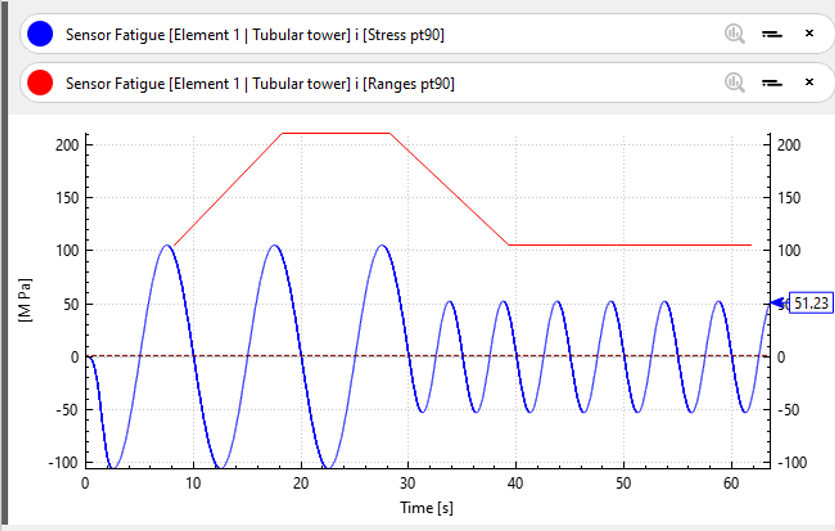
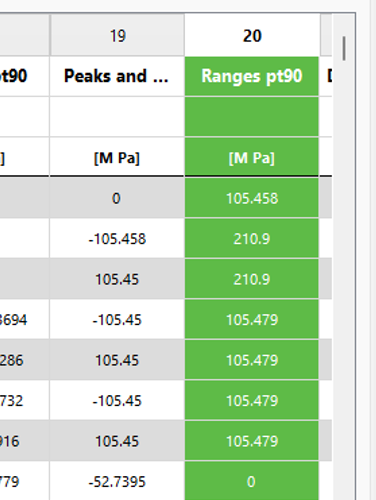
After 60 seconds, the Rainflow conting algorithm will have counted 2 cycles of range
$$2A_1$$
and 5 cycles of range
$$2A_2$$
Note
: stresses that are below the
Stress ranges filter
limit will not be considered by the algorithm.
1.3 Evaluate the damage of each new stress range
Each new stress range is then checked against the selected S-N curve. If we take the stress range from the first example above at
$$2A_1=210.9\text{ MPa}$$
, we can plot this in the S-N curve to see what the number of cycles that would lead to failure at that stress level is:
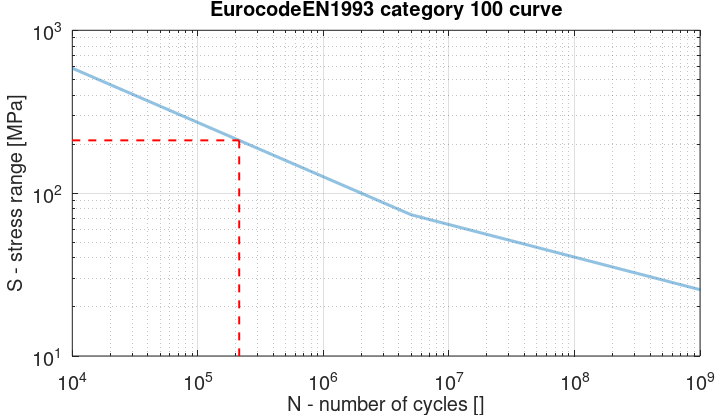
In this case, and assuming a Eurocode EN1993 S-N curve of category 100, it would take about
$$N=213{\ }000$$
cycles to reach failure. This means that this range will produce a damage of
$$d=1/N=4.68\cdot10^{-6}$$
Following the
Palmgren-Miner linear damage hypothesis
, the damages produced by each new range (i.e. new stress cycle) are added together to obtain an
accumulated damage
.
1.4 Fatigue life
The
Fatigue life
is computed at each time step depending on how long the simulation has been running for. If the accumulated damage at time
$$t$$
is
$$d$$
, the fatigue life (in seconds) will simply be
$$f=t/d$$
.
This can be understood as follows: the fatigue life is the time it takes to reach failure, which by definition happens when
$$d=1$$
. Therefore (and assuming linear damage), if it took
$$t$$
seconds to reach an accumulated fatigue damage
$$d$$
, it will take
$$t/d$$
seconds to reach a damage of 1.
This is illustrated in the figure below, again from the first example above:
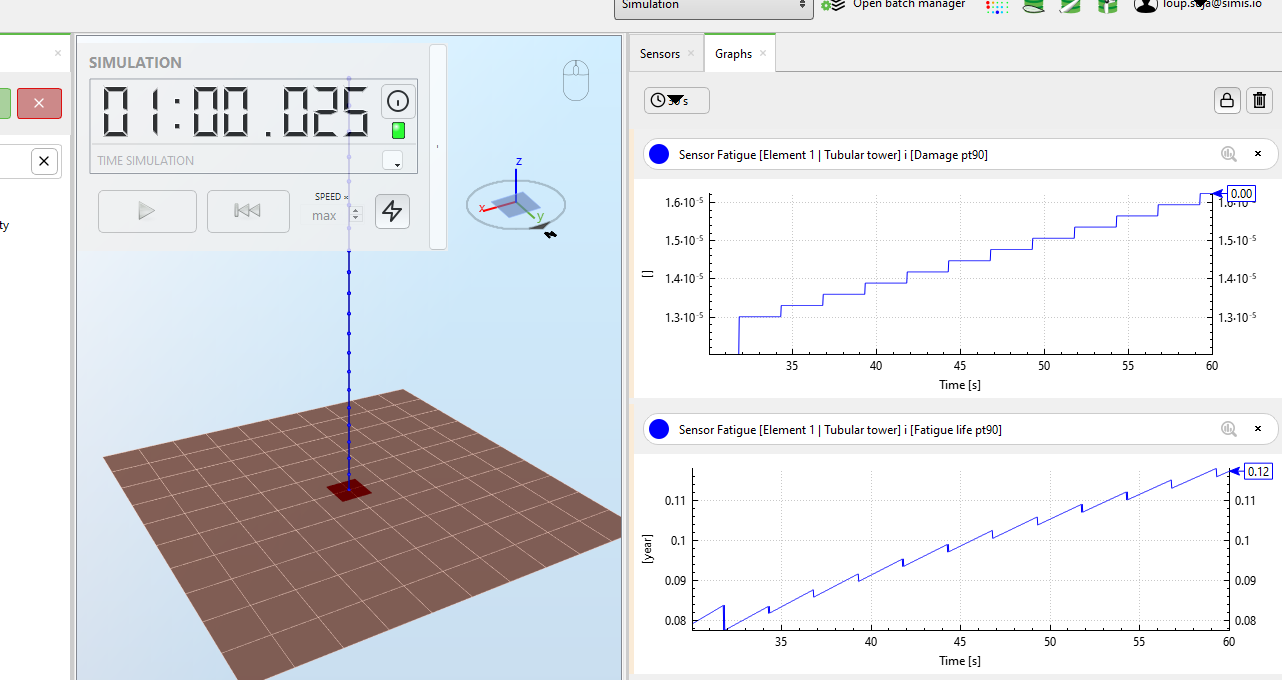
The accumulated damage after
$$t=60\text{ s}$$
is
$$d=1.6236\cdot10^{-5}$$
, therefore the fatigue life in years will be
$$F_L = t/(d\cdot3600\cdot24\cdot365)=0.117\text{ years}$$
Note
: the fatigue damage is discontinuous (as seen in the figure above) because its value changes every time a new range is added, i.e. every time a new load cycle has happened.
2 Fatigue life from histogram
This fatigue life estimation is done once the output file of the sensor os exported, or once the batch is finished (for batch simulations).
2.1 Retrieving stress time series
At the end of the batch, the
stress time series
, which include the
SCFs
defined by the user or pre-computed by Ashes, are retrieved from the results.
2.2 Performing the Rainflow counting algorithm
The stress time series goes through the
Rainflow counting algorithm
. The output of the counting is a load cycle histogram, that shows the number of cycles at a given stress range that happened during the simulation. The figure below is an example of such a histogram.
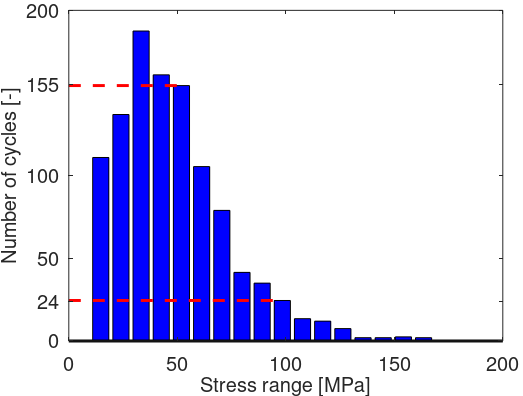
Note:
the table containing this data can be found in the output file of the
Fatigue sensor
(and currently not in the fatigue report)
2.3 Computing the damage
Once the histogram has been derived, the S-N curve is used to obtain the damage from each load cycle bin. Following the same procedure as in section 1.3 above, the figure below shows that the damage for the 50 MPa bin is
$$d_{50}=1/3.4\cdot10^7=2.9\cdot10^{-8}$$
and the damage for the 100 MPa bin is
$$d_{100}=1/2\cdot10^6=5\cdot10^{-7}$$
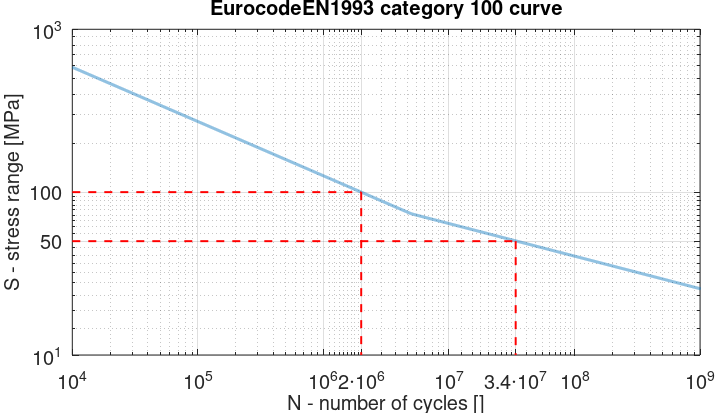
Following the
Palmgren-Miner linear damage hypothesis
, the damages produced by each bin are added together to obtain an accumulated damage.
2.4 Combining damages for the whole batch
At this point we have estimated the accumulated damage for one load case only. To obtain the combined damage for the batch, the damages from all load cases are multiplied by the porbability of occurrence of that load case (which is set in the batch) and summed up.
The fatigue life is then obtained by following the same procedure as in section 1.4: if the combined damage for the load cases is
$$d$$
and the simulation duration is
$$t$$
, then te fatigue life in seconds is
$$t/d$$
.
The
Fatigue life from histogram
estimate is the one that is provided in the Fatigue report produced after a batch run.
Note
: the two estimates might be slightly different. This is because the ranges are binned in the
from histogram
approach. The bin definition can be found in the sensor output