MacCamy-Fuchs
The
Morison equation
used in Ashes to compute hydrodynamic loads on support structures for wind turbines does not account for the fact that the structure will diffract the incoming waves. This assumption is valid if the wavelength is much larger than the diameter of the element onto which loads are calculated.
Faltinsen (1990)
suggests that diffraction effects must be taken into account when the wavelength
$$\lambda$$
is less than five times the diameter
$$D$$
, or for
$$D/\lambda>0.2$$
.
According to
IEC-61400-3-1 (2019)
, diffraction effects can be taken into account by using the
MacCamy-Fuchs
theory. The MacCamy-Fuchs loads reduce to the Morison equation when the wavelength is much larger than the element diameter.
Note:
it is a common misconception to think that the loads from the MacCamy-Fuchs theory are
always
lower than those from the Morison equation. For long wavelength, the loads will actually be higher (as will be seen in the figure below). However, for these long wavelengths, the MacCamy-Fuchs theory is generally not needed as diffraction effects are not dignificant.
It is therefore correct to say that the loads from the MacCamy-Fuchs theory are lower than those from the Morison equation
when diffraction effects are significant
, i.e. for
$$D/\lambda>0.2$$
.
Such theory can be implemented by modifying the inertia coefficient of the Morison equation
$$C_M$$
with the equation
$$C_M = \frac{4}{\pi (kr)^2\sqrt{A_1(kr)}}$$
where
$$k$$
is the wave number and
$$r$$
is the radius of the element.
$$A_1$$
is equal to
$$A_1(kr) =J_1'^2(ka)+Y_1'^2 $$
where
$$J_1'$$
is the derivative of the Bessel function of the first kind of order 1 and
$$Y_1'$$
is the derivative of the Bessel function of the second kind of order 1.
Note:
these equations are often provided with the wave number
$$k$$
and the radius
$$r$$
, rather than
$$\lambda$$
and
$$D$$
. These are simply linked through the equation
$$\pi D/\lambda = kr$$
.
Note that Bessel functions are relatively difficult to evaluate. In Ashes, we use a curve fitting to get the inertia coefficient, which is then defined as
$$C_M = \frac{0.581(kr^2)+0.718kr+0.780}{(kr)^3-0.256(kr)^2+0.381kr+0.389}$$
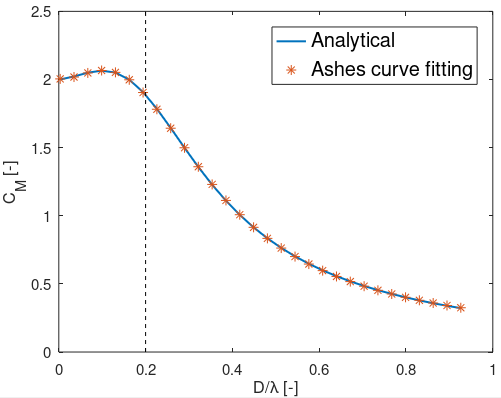
The figure below shows the analytical solution and the curve fitting approximation done in Ashes. The dotted line shows the limit above which diffraction effects must be included.
This figure confirms that for
$$D/\lambda>0.2$$
, the loads from the MacCamy-Fuchs theory are lower than those from the Morison equation.
Note:
when using the MacCamy-Fuchs theory, the inertia coefficient for long waves (i.e. small
$$D/\lambda$$
) will always be 2
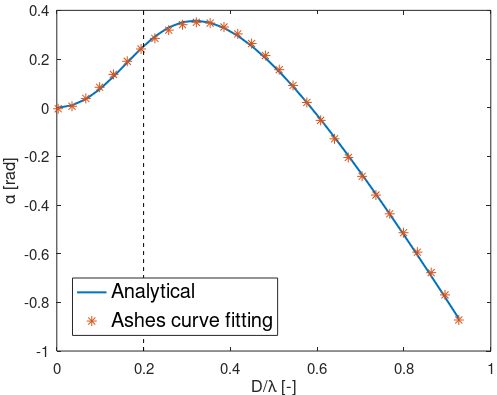
Similarly to the modification of the inertia coefficient, the MacCamy-Fuchs correction introduces a phase difference with the Morison equation. According to
IEC-61400-3-1 (2019)
, the phase difference is given as
$$\alpha(kr) = \arctan\left(\frac{J_1'(ka)}{Y_1'(ka)}\right)$$
In Ashes, we use a curve fitting to get the phase difference, which is then defined as
$$\alpha(kr)=-0.0752(kr)^5+0.615(kr)^4-1.7372(kr)^3+1.6221(ka)^2-0.0705kr-0.0038$$
The figure below shows the analytical solution and the curve fitting approximation done in Ashes. The dotted line shows the limit above which diffraction effects must be included.
Note:
using a 5
th
order polynomial for the curve fitting might seem like a bit of an overkill, but this was necessary to ensure that for long waves (i.e. small kr), there is no phase difference between the Morison and the MacCamy-Fuchs formulations. This is relevant when applying the MacCamy-Fuchs theory while using irregular waves, as some waves will be in the long wavelength regime
The implementations of the MacCamy-Fuchs theory in Ashes is verified in the
MacCamy-Fuchs test
.