Fatigue test
1 Test description
This test uses a constant known cross-section tubular tower fixed onto the ground. Wind and gravity loads are disabled, a point load is applied to the top of the tower. For different loads and fatigue input, the stresses and corresponding fatigue lifes are compared against the analytical solution.
Note that this configuration is also used for the blade fatigue test, where a blade with identical characteristics is used.
2 Model
The model used for this test is shown in the figure below:
The tower has a length
$$L=100\text{ m}$$
, an outer radius
$$R=2.5\text{ m}$$
and a thickness
$$t=0.03 \text{ m}$$
. The second moment of area of the cross section is
$$I = 1.682\text{m}^4$$
. The material is infinitely stiff.
A stress filter of 1 MPa is applied, so any stress ranges below that value are not taken into consideration for fatigue calculations.
3 Analytical solution
3.1 Static pull
A force
$$F=289.3\text{ kN}$$
is applied on top of the tower in the x-direction, corresponding to the 1st principal direction of the top element. That will generate a response bending moment at the bottom of the tower arond the 2nd principal direction of the bottom element
$$M = L\cdot F=-28.93\text{ MNm}$$
. The stress will then be
$$\sigma=R\cdot M/I=-50\text{ MPa}$$
.
3.2 Oscillating load
The same force as in the previous is applied as an oscillating load with a period
$$T = 15.768\text{ s}$$
. This period is chosen because it will produce two million cycles in one year.
For fatigue calculations, no Stress Concentration Factor is applied and the SN curve is the EurocodeEN1993 category 100 curve. By definition,
category 100
means that an oscillating stress of range
$$r=100\text{ N}\cdot\text{mm}^2=100\text{ MPa}$$
(produced by a stress of amplitude
$$a=50\text{ MPa}$$
) will produce 100% damage at two million cycles. This is illustrated in the figure below:
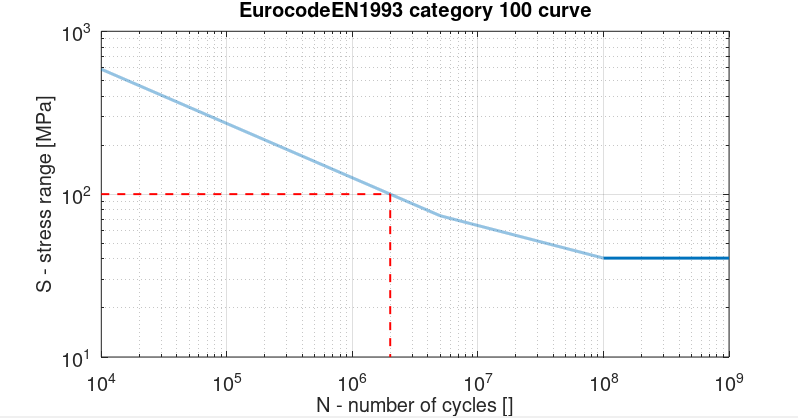
In the present test, two million cycles correspond to one year. The damage will be 100% after one year, which means that the fatigue life of the studied structure is
$$f_l=1\text{ year}$$
4 Results
A time simulation of 150 seconds is run for each load case and the last 20% are compared to the analytical solution. If the results from Ashes are within 0.5% of the analytical solution, the test is considered passed.
The report of this test can be found on the following link:
The report of the test with the blade can be found on the following link: