Oye's dynamic stall model

This section explains how the lift coefficient C L is adjusted to account for dynamic stall effects following the work by  Øye (1991a) .



Note : the dynamic stall model is not relevant for cylinders

In this work, the dynamic stall is modelled through a so called separation function 
$$f$$
  such as 
$$C_L(\alpha) = fC_{L,inv}(\alpha) + (1-f)C_{L,fs}(\alpha)$$
 (1)
where 
$$C_{L,inv}$$
 is the lift coefficient for inviscid flow without separation and 
$$C_{L,fs}$$
 is the lift coefficient for fully separated flow. In order to solve this equation, we first apply it to static conditions, such as
$$C_L^{st}(\alpha) = f^{st}C_{L,inv}^{st}(\alpha) + (1-f^{st})C_{L,fs}^{st}(\alpha)$$
 (2)
where the superscript 'st' refers to the static solution.
$$C_L^{st}(\alpha)$$
corresponds to the value looked up in the polar and 
$$C_{L,inv}^{st}(\alpha)$$
 is obtained by extrapolating the linear region of the lift curve, as illustrated below. Note that by definition, 
$$C_{L,inv}^{st}=C_{L,inv}$$
 and
$$C_{L,fs}^{st}=C_{L,fs}$$
. 

As suggested by Hansen et al. (2004f) , 
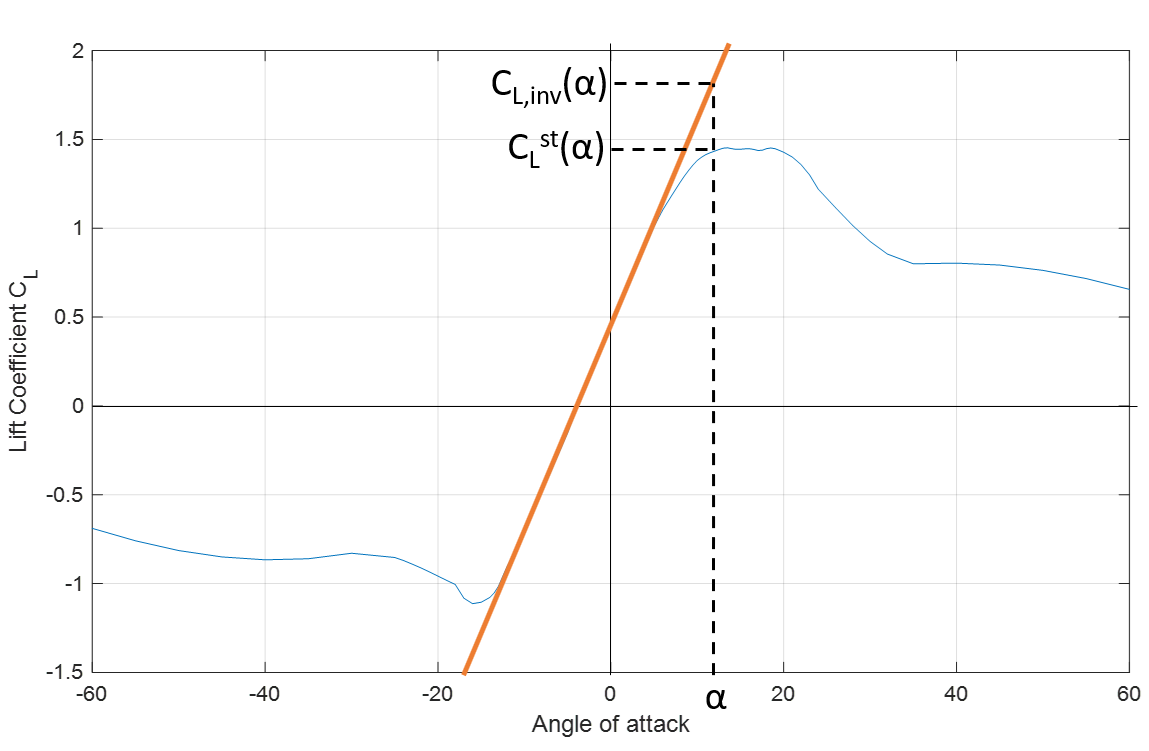
$$f^{st}$$
 is given by
$$f^{st}=\left(2\sqrt{\frac{C_L^{st}}{C_{L,inv}^{st}}}\right)^2$$
 (3)
Note that the theoretical upper limit for 
$$f^{st}$$
 is 1. If a higher value is obtained, then 
$$f^{st}=1$$
 is taken. Once 
$$f^{st}$$
 is calculated, 
$$f$$
 is computed by assuming that it comes back to the static value following
$$\frac{df}{dt}=\frac{f^{st}-f}{\tau}$$
 (4)
This forumla can be analytically integrated to give
$$f(t)=f^{st}(t)+f(t-\Delta t)-f^{st}(t)\exp{\frac{-\Delta t}{\tau}}$$
 (5)
where 
$$\Delta t$$
 is the time step of the simulation and 
$$f(t-\Delta t)$$
 corresponds to the separation function at the previous time step. 
$$\tau$$
is a time constant taken as
$$\tau = \frac{4c}{|W|}$$
 (6)
where 
$$c$$
 is the chordlength and 
$$W$$
 is the relative velocity.
Once 
$$f$$
 has been determined, the next step to solve equation (1) is to calculate 
$$C_{L,fs}(\alpha)$$
 and 
$$C_{L,inv}(\alpha)$$
. By reorganizing equation (2), we can express 
$$C_{L,fs}$$
 as
$$C_{L,fs}(\alpha)=\frac{C_L^{st}(\alpha)-f^{st}C_{L,inv}(\alpha)}{1-f^{st}}$$
 (7)
If 
$$f^{st}=1$$
, then 
$$C_{L,fs}$$
 is computed as 
$$C_{L,fs}(\alpha) = C_L^{st}(\alpha)/2$$
Once 
$$C_{L,inv}(\alpha)$$
 and 
$$C_{L,fs}(\alpha)$$
 have been calculated, they are insterted in equation (1) to determine the lift coefficient.