Nonlinear springs
Ashes gives the possibility to implement
nonlinear springs
, i.e. springs with a stiffness that depends on the displacement of the node. Nonlinear springs can be applied as
translational
or
rotational
springs.
Nonlinear springs are input in the text file describing the imported support structure (see
Support section files
) as
look-up tables
of displacement vs force, so-called
P-y curves
(see
API (2011)
). When a node is displaced, it experiences a force corresponding to the value of the projection of the displacement in the spring direction in the look-up table, in the opposite direction of the displacement. If a displacement falls between two values of the look-up table, the force is linearly interpolated between the closest values.
The figure below illustrates an example of P-y curve:
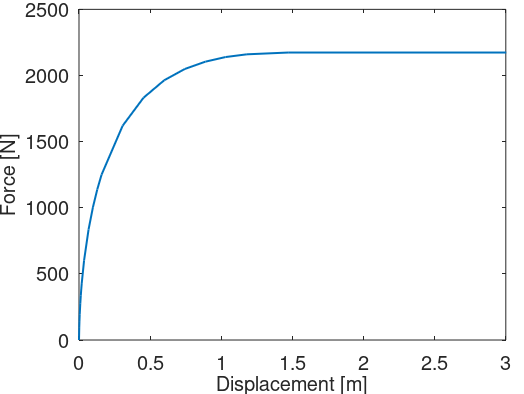
Note:
in Ashes, the look-up table is given as
Force against Displacement
(and not pressure against displacement).
Nonlinear springs can be applied in all six degrees of freedom, which enables the implementation of the
PISA model
(see
Byrne et al. (2019)
).
When a nonlinear spring is applied to a model, the
Support sensor
will show the output
Stiffness
. If a look-up table contains a force
$$F$$
and a displacement
$$d$$
defined as follows
$$F=[F_1,F_2,F_3\cdots F_n]$$
$$d=[d_1,d_2,d_3,\dots d_n]$$
then for a displacement
$$d_x$$
such that
$$d_i\leq d_x < d_{i+1}$$
, the stiffness
$$K(d_x)$$
is defined as
$$K(d_x)=\frac{F_{i+1}-F_{i}}{d_{i+1}-d_{i}}$$
Note:
the same definition applies for nonlinear rotational springs: a
rotational stiffness
is computed from the moment and the rotational displacement in the table