$$a_c = 0.2$$
. This is also cited by
Hansen (2008d)
. This limit seems to have been abandonned.
Glauert correction
The derivation of the momentum theory for an ideal wind turbine (see for example
Hansen (2008d)
) states that the thrust coefficient
$$C_T$$
and te axial induction factor
$$a$$
are linked through the following formula:
$$C_T=4a(1-a)$$
It is common to apply the so-called
Prandtl correction
(see
Steady BEM
) by adding the tip and hub loss factor
$$F_P$$
such that
$$C_T = 4a(1-a)F_P$$
When a turbine is operating with high axial induction factors (this can be the case at high TSR, which can happen at low sind speeds with a constant RPM), the basic assumptions of the BEM theory break down and the thrust coefficient can no longer be obtained from the above equation. In this situation, a different formula need to be used to determine the thrust coefficient. Several correcions exist, and the value of the axial induction factor from which the correction needs to be applied (called the
Critical Glauert Value
ant noted
$$a_c$$
) van vary with the correction used.
Ashes offers the choice between two well-known methods:
Emprical correction
This correction is based on
Hansen (2008d)
and states that the thrust coefficient can be computed as
$$C_T=\left\{\begin{array}{ll}4a(1-a)F_P&\text{for }a\leq 1/3\\ 4a\left(1-0.25(5-3a)a\right)F_P&\text{for }a>1/3\end{array}\right.$$
Wilson and Walker correction
This correction can be found in
Spera (2009)
:
$$C_T=\left\{\begin{array}{ll}4a(1-a)F_P&\text{for }a\leq a_c\\ 4\left(a_c^2+(1-2a_c)a\right)F_P&\text{for }a>a_c\end{array}\right.$$
$$a_c$$
should be greater or equal to
$$1/3$$
.
Note:
in a previous edition of
Spera (2009)
(the 1994 edition), the recommendation is to use
The graph below shows how the corrections compare:
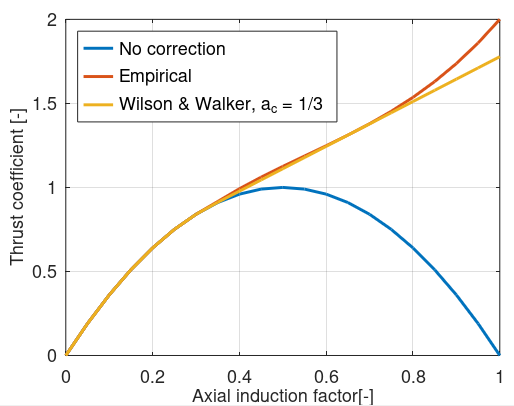
Note that in Ashes, we follow the algorithm descrbed by
Hansen (2008d)
which uses the
Glauert correction factor
$$f_g$$
such that
$$C_T=4a(1-f_g\cdot a)F_P$$
This enables us to reformulate the Glauert correction as follows:
Empirical correction
:
$$f_g=\left\{\begin{array}{ll}1&\text{for }a\leq 1/3\\ 0.25(5-3a)&\text{for }a>1/3\end{array}\right.$$
Wilson and Walker correction
$$f_g=\left\{\begin{array}{ll}1&\text{for }a\leq a_c\\ \frac{a_c}{a}\left(2-\frac{a_c}{a}\right)&\text{for }a>a_c\end{array}\right.$$