Albert Betz showed in 1919 that the theoretical maximum power coefficient of a wind turbine was 17/29, about 59.3%, widely known as the
Betz limit
(
https://en.wikipedia.org/wiki/Betz%27s_law
). Current turbines have maximum power coefficients of about 50%.
Note
that Ashes uses the
Blade length
when computing the power coefficient. This might yield to unphysically high power coefficients when using unrealistically swept blades.
C P - Power coefficient
The power coefficient is defined as the ratio of the power produced by a rotor over the available power at a given
instant. It is a measure of the efficiency of a rotor and it is given by the equation
$$C_P(t) = \frac{P(t)}{P_{avail}(t)} = \frac{P(t)}{\frac{1}{2}\rho A V(t)^3}$$
where
-
$$P(t)$$is the power produced by the turbine at the instant$$t$$
-
$$P_{avail}(t)$$is the available power at the instant$$t$$
-
$$\rho$$is the density of the air
-
$$A$$is the projected area of the rotor
-
$$V$$is the velocity of the wind normal to the rotor at the instant$$t$$
The power coefficient depends on the characteristics of the rotor (hub radius, blade length and shape, cone angle, etc) and the state of the control system (rotational speed of the rotor, pitch angle of the blades, etc).
It is common to analyse the performance of a wind turbine by plotting the Cp as a function of the tip speed ratio (commonly noted TSR or
$$\lambda$$
) for a given pitch angle. The tip speed ratio is defined as the ratio of the velocity of the tip of the blade over the velocity of the wind normal to the rotor, and is thus given by the equation
$$TSR = \frac{tip speed}{wind speed}=\frac{\Omega\frac{2\pi}{60}R}{V}$$
The image below shows the Cp curve for the NREL 5 MW rotor at 0 pitch.
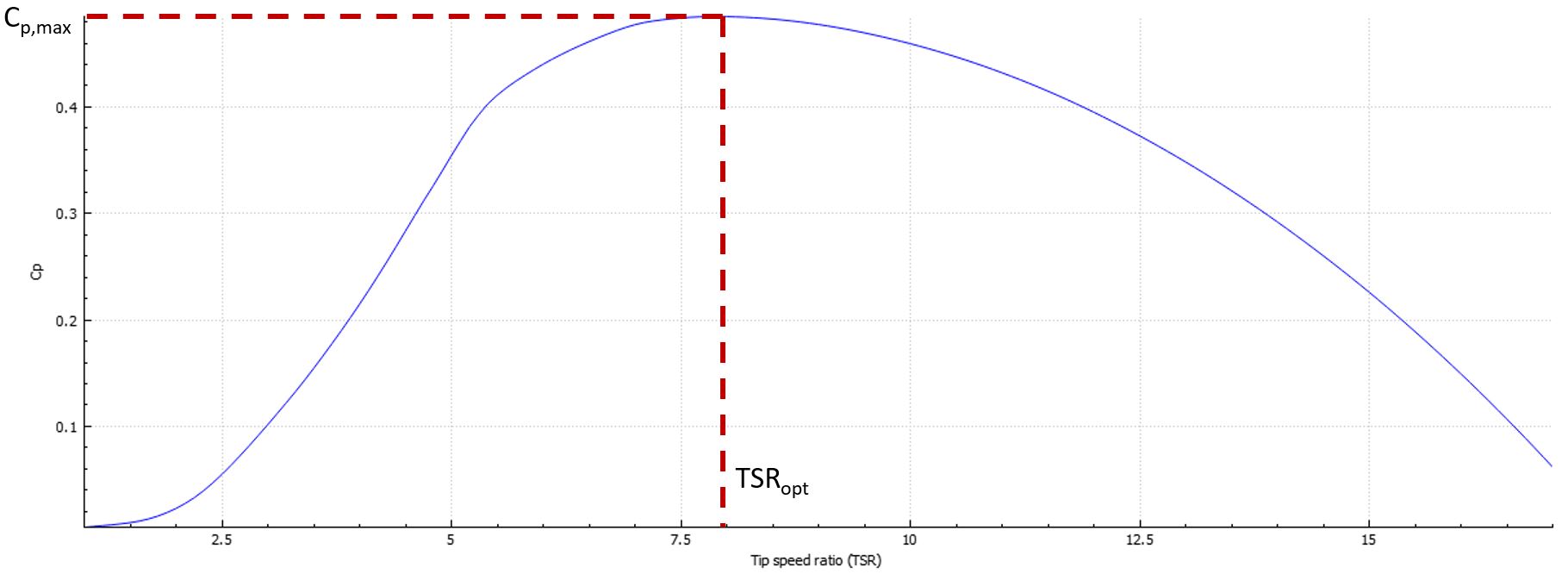
This curve is important because it enables us to establish which is the TSR at which the rotor has its highest Cp. This TSR is called the
optimal TSR
. When the turbine is operating below rated conditions, the control strategy is generally to adjust the rotational velocity of the rotor as a function of the wind velocity so that the rotor is at its optimal TSR.