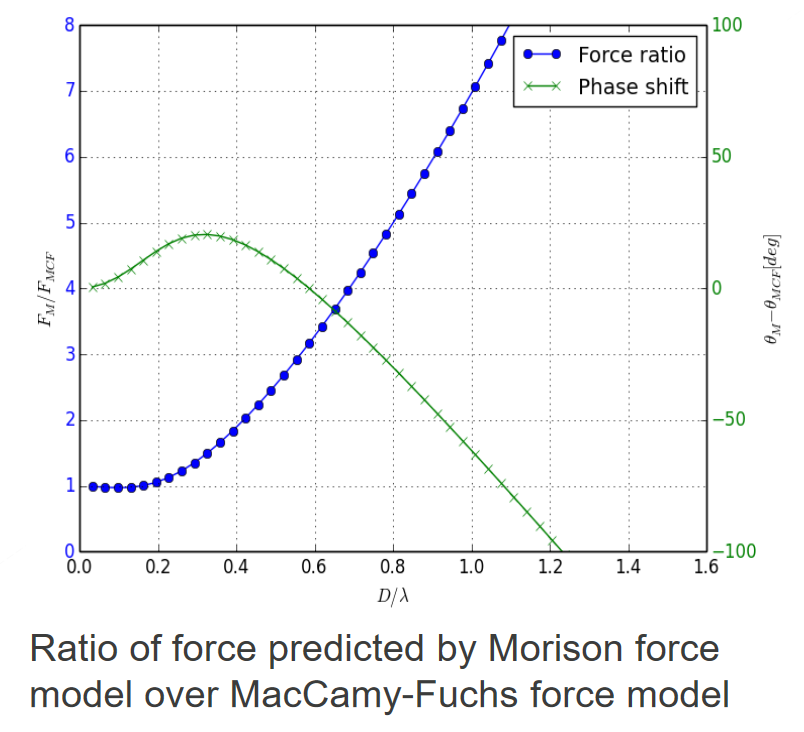
MacCamy Fuchs Benchmark
This test ensures that the loads produced using the MacCamy-Fuchs theory in Ashes are correct. To do so, we compare results produced by Ashes to those published on slide 11 of the presentation that can be found on this page:
https://www.sintef.no/globalassets/project/eera-deepwind-2018/presentations/f_pierella.pdf
. This slide compares the amplitude and phase of hydrodynamic loads produced by the inertia term of the Morison equation and the MacCamy-Fuchs theory. The relevant figure is reproduced below:
1
Test description
This test uses a monopile in regular waves. The monopile is composed of two elements: one that does not experience any hydrodynamic loads and that is fixed and one that experiences hydrodynamic loads. To check that the loads are correctly calculated, the
Shear force
from the
Beam element sensor
of the fixed element is checked. The monopile is infinitely stiff, and there are no other loads than the hydrodynamic loads. Therefore this shear force will be equal to the hydrodynamic loads.
The results used to benchmark Ashes are produced as follows:
-
the hydrodynamic loads on the structure are computed using the analytical solution, as done in the
Morison test
-
the amplitude is scaled according to the ratio shown in the figure above
-
the phase is shifted by the phase difference according to the figure above
2
Model
The model is illustrated in the figure below.
The default model for this test has a diameter
$$D = 6\text{ m}$$
and the element with hydrodynamic loads has a length
$$dz = 5\text{ m}$$
. In this test, we neglect the drag part of the Morison equation. The water depth is
$$h = 20\text{ m}$$
, and the element experiencing hydrodynamic loads extends from a vertical coordinate
$$z = -5\text{ m}$$
to the mean sea level at
$$z = 0$$
.
The acceleration due to gravity is
$$g = 9.80665\text{ m}\cdot\text{s}^{-2}$$
and the water density is
$$\rho = 1026.9\text{ kg}\cdot\text{m}^{-3}$$
.
3
Benchmarked solution
We only consider linear regular waves in these tests. These are defined by a wave length
$$L$$
and a wave height
$$H$$
. The wave number is defined as
$$k = 2\pi/L$$
. The wave frequency
$$\omega$$
can be obtained through the linear disperson relationship, such that
$$\omega^2 = gk\tanh(kh)$$
, and the wave period is equal to
$$T = 2\pi/\omega$$
.
The force at time
$$t$$
and height
$$z$$
is given by the inertia term of the Morison equation. Since we consider a fixed, infinitely stiff structure, the Morison equation given in
Wave loads
can be reduced to
$$F(z,t) = \frac{1}{K}\cdot\rho C_M\pi\frac{D^2}{4}a(z,t) dz$$
where
$$a(z,t)$$
is the wave particle acceleration. The ratio
$$K$$
is taken from the figure above.
The particle acceleration is given by
$$a(z,t) = \omega^2\frac{H}{2}\frac{\cosh\left(k(z+h)\right)}{\sinh(kh)}\cos(\omega t - \alpha(kD))$$
The difference in phase between the Morison equation and the MacCamy-Fuchs correction
$$\alpha(kD)$$
is taken from the figure above..
Note:
in Ashes, the hydrodynamic load is computed at the midpoint of the corresponding element. For this test, since the element goes from
$$z = -5\text{ m}$$
to the mean sea level, the load will be compute using the kinematics at
$$z = -2.5\text{ m}$$
For each load case, only the wavelength
$$L$$
and the wave height
$$H$$
are changed. The table below summarises the different load cases that are run and the expected results.
|
Load case
|
Wavelength [m]
|
Wave heigh [m]
|
Diameter to wavelength ratio (from figure) [-]
|
Phase shift (from figure) [deg]
|
Ratio Morison amplitude over MacCamy-Fuchs amplitude (from figure) [-]
|
Amplitude from the Morison load (analytical) [kN]
|
Expected amplitude from the MacCamy-Fuchs correction [kN]
|
|
L = 60 ,
|
60
|
3
|
0.1
|
4.7
|
0.97
|
344
|
344
|
|
L = 30 m
|
30
|
1.5
|
0.2
|
14.6
|
1.07
|
265
|
248
|
|
L = 20 m
|
20
|
1
|
0.3
|
20.3
|
1.3
|
204
|
157
|
|
L = 15 m
|
15
|
0.75
|
0.4
|
17.8
|
1.8
|
157
|
87
|
|
L = 12 m
|
12
|
0.6
|
0.5
|
9.4
|
2.5
|
121
|
48.4
|
|
L = 10 m
|
10
|
0.5
|
0.6
|
-2.0
|
3.3
|
93
|
28
|
|
L = 8.57 m
|
8.57
|
0.43
|
0.7
|
-15.3
|
4.1
|
72
|
18
|
|
L = 7.5 m
|
7.5
|
0.375
|
0.8
|
-30.2
|
5.0
|
55
|
11
|
|
L = 6.67 m
|
6.67
|
0.33
|
0.9
|
-45.7
|
5.9
|
42
|
7.1
|
|
L = 6 m
|
6
|
0.3
|
1
|
-67.1
|
7.0
|
33
|
4.7
|
4
Results
A simulation of 30 seconds is run for each load case. The results are considered passed if the results from Ashes are within 5% of the expected solution.
The report for this test can be found on the following link: