DTU 10-MW blade eigenfrequencies
1 Test description
In this test we compare the eigenfrequencies of an isolated DTU 10-MW blade given in Table 6.4 of
Bak et al. (2013)
to results obtained in Ashes.
2 Model
The DTU 10-MW blade can be found in the
Blade database
. The blade is fixed at its root.
3 Benchmarks
In the following sections, the different modeshapes are illustrated and the expected eigenfrequencies as listed in
Bak et al. (2013)
are given.
3.1 First flapwise mode
The expected eigenfrequency is
$$f_1 = 0.61 \text{ Hz}$$
.
This mode shape is illustrated in the figure below:

3.2 First edgewise mode
The expected eigenfrequency is
$$f_2 =0.93\text{ Hz} $$
.

3.3 Second flapwise mode
The expected eigenfrequency is
$$f_3 =1.74\text{ Hz}$$
.
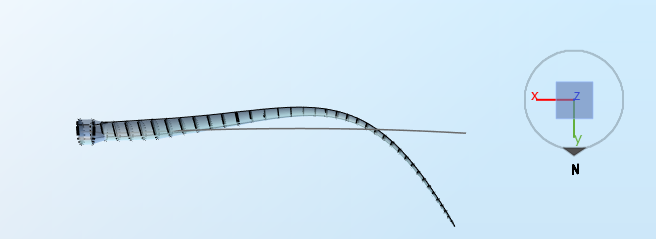
3.4 Second edgewise mode
The expected eigenfrequency is
$$f_4 = 2.76\text{ Hz}$$
.
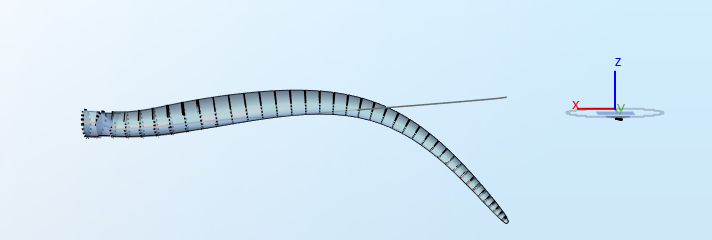
3.5 Third flapwise mode
The expected eigenfrequency is
$$f_5 =3.57\text{ Hz}$$
.

3.6 Third edgewise mode
The expected eigenfrequency is
$$f_6 =6.66\text{ Hz}$$
.
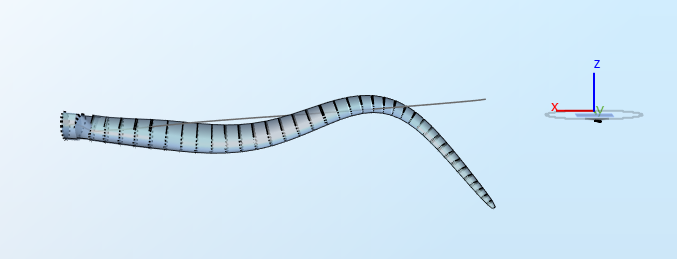
3.7 Fourth flapwise mode
The expected eigenfrequency is
$$f_7=6.11\text{ Hz}$$
.

4 Results
The test is considered passed if the results from Ashes are within 5% of the data from the specification document. A bar plot comparing the eigenfrequncies is available on the following link: