Regular waves
The wave kinematics of regular waves in Ashes are computed used linear theory, also called Airy wave theory. In this theory, the water is considered inviscid, incompressible and irrotational. By assuming that water is inviscid, incompressible and irrotational, the water can then be described by a velocity potential as follows (see
Faltinsen (1990)
):
$$\Phi = \frac{gA}{\omega}\frac{\cosh\left[k(z+h)\right]}{\cosh(kh)}\cos(\omega t +k_xx+k_yy)$$
where
$$x, y, z$$
are spatial coordinates in a Cartesian reference system [m]
$$t$$
is the time coordinate [s]
$$A$$
is the wave amplitude [m]
$$g$$
is the acceleration due to gravity [m.s
-2
]
$$\omega$$
is the wave circular frequency, [rd.s
-1
]
$$k$$
is the magnitude of the wave number vector [rd.m
-1
]
$$h$$
is the water depth (for a flat bottom) [m]
$$k_x,k_y$$
are the horizontal components of the wave number vector [rd.m
-1
]
Note:
it is common to use the
wave height
$$H=2A$$
and the
wave period
$$T=2\pi/\omega$$
when describing a regular wave.
Note:
the
plus
sign in the cosine part of the equation implies that the waves travel from positive values to negative values. For instance, for the default models in Ashes, the wave crests move from positive y-values to negative y-values.
The wave number
$$k$$
and the wave frequency
$$\omega$$
are linked through the linear dispersion relationship
$$\omega^2=gk\cdot tanh(kh)$$
For a wave coming at an angle
$$\theta$$
with respect to the North direction, the directional wave number are then given by
$$k_y = k\cos{\theta}$$
and
$$k_x = k\sin{\theta}$$
.
If
$$\theta=0$$
, the waves come from the positive y value. If
$$\theta=90 ^\circ$$
, they come from the positive x value.
The figure below illustrates waves coming at
$$\theta = 20^\circ$$
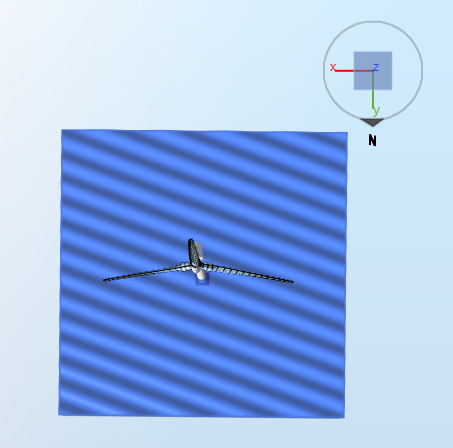
The wave elevation is then given by
$$\zeta = A\cdot sin(\omega t + k_xx + k_yy)$$
The water particle velocity in the x, y and z direction are respectively
$$u=\frac{\partial \Phi}{\partial x}$$
$$v=\frac{\partial \Phi}{\partial y}$$
$$w=\frac{\partial \Psi}{\partial z}$$
The water particle accelerations are the time derivatives of the water particle velocities.
The figure below illustrates the geometrical definitions of the wave:
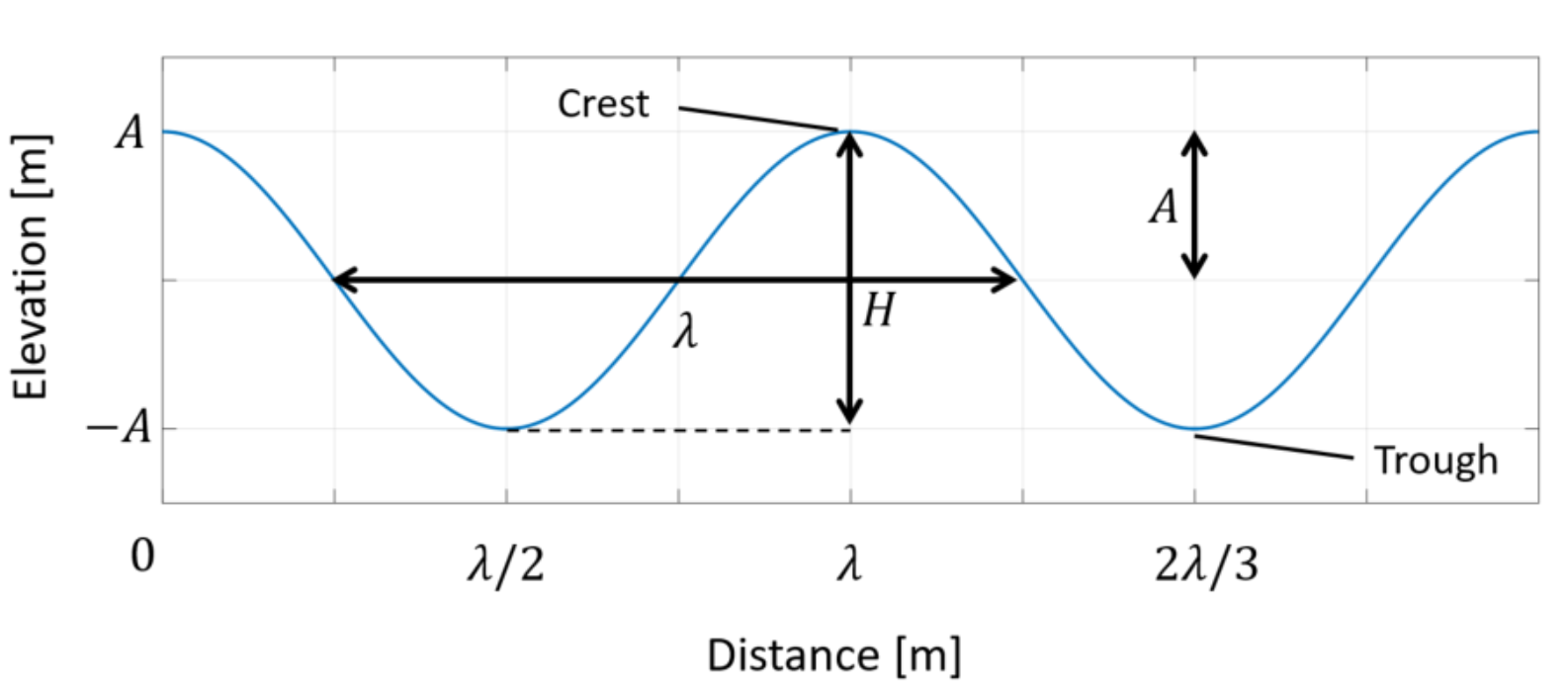
1
Deep water approximation
It is common to distinguish between
Deep
or
Infinite
water and
Finite
water depending on the wave characteristics and water depth. In deep waters, it is assumed that the sea bed does not affect the wave kinematics. By defining the wave length
$$\lambda$$
as
$$\lambda = 2\pi/k$$
, deep water is assumed when
$$\lambda/h>0.5$$
. Under these conditions, the approximation
$$kh\gg 1$$
is made. The expression for the velocity potential then becomes
$$\Phi=\frac{gA}{\omega}e^{kz}\cos(\omega t -k_xx-k_yy)$$
and the dispersion relationship becomes
In Ashes, the parameter
Depth approximation
in the
Sea
part enables you to select whether deep water waves kinematics are computed based on this approximation or based on the finite water equations.
2
Regular wave characteristics
When modeling regular waves, It is common to give as input the wave height
$$H$$
, the wave period
$$T$$
and the water depth
$$h$$
. Several characteristics of the linear wave can be derived from these input, and are available in the
Information pane o
f the
Regular wave
part. The following section shows how these characteristics are derived:
The
wave length
is
$$\lambda = 2\pi/k$$
The
wave number
is obtained by solving the dispersion relationship
$$\omega^2=gk\cdot tanh(kh)$$
The
circular frequency
is
$$\omega = 2\pi/T$$
The
wave steepness
is
$$H/\lambda$$
The
critical wave height
$$H_c$$
corresponds to the theoretical maximum height that a wave can have before it breaks. For deep water,
$$H_c = \lambda/7$$
and for finite water
$$H_c = 0.78h$$
The
wave (phase) velocity
is
$$c=\lambda/T$$
The
wave group velocity
is
$$c_g= \frac{c}{2}\left(1+\frac{2kh}{\sinh(2kh)}\right)$$

