How to use Rayleigh damping
Ashes offers the possibility to use
Rayleigh damping
to dampen out the response of the structure. The Rayleigh damping characteristics can be changed in the
Damping
section of the
Analysis
tab of the
Analysis parameters
window.
Rayleigh damping is implemented following the equations given in the
Damping
section. This produces a damping ratio equal to
$$\xi = 0.5\left(\frac{\mu}{2\pi f}+\lambda2\pi f\right)$$
$$\xi$$
is the damping ratio,
$$f$$
is the frequency of the response and
$$\mu$$
and
$$\lambda$$
are the mass and stiffness damping coefficients, respectively. This method produces a damping ratio that is dependent on the frequency of the response. Given that there are 2 coefficients that can be input by the user, it is possible to select those coefficients so that 2 frequencies correspond to 2 damping ratios selected by the user. It is common to specify the damping ratios of the first two eigenmodes of the structure, which yields a system of two equations where the unknowns are
$$\mu$$
and
$$\lambda$$
, as follows:
$$\xi_1=0.5\left(\frac{\mu}{2\pi f_1} + \lambda 2\pi f_1\right)$$
$$\xi_2=0.5\left(\frac{\mu}{2\pi f_2}+\lambda 2\pi f_2\right)$$
where
$$\xi_1$$
and
$$\xi_2$$
are the damping ratios of the 1
st
and 2
nd
mode shapes, respectively and
$$f_1$$
and
$$f_2$$
are the 1
st
and 2
nd
eigenfrequencies, respectvely. For example, within the OC5 project,
Robertson et al. (2016e)
reports the following characteristics for the support structure of the NREL 5 MW turbine:
| Eigenfrequency [Hz] | Damping ratio [-] | |
| 1 st mode | 0.28 | 0.017 |
| 2 nd mode | 2.0 | 0.027 |
In order to achieve these characteristics, the damping ratios and eigenfrequencies are input into the system of two equations. The mass and stiffness coefficients that produce these characteristics are
$$\mu=0.047$$
and
$$\lambda=0.004$$
. This is illustrated in the figure below:
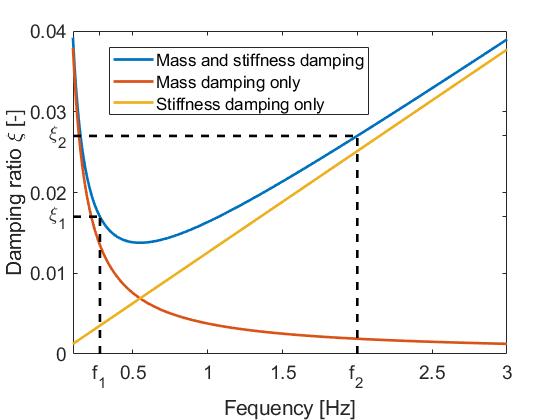
Note that with this method, it is not possible to specify the damping ratios of more that 2 frequencies. For example, in this case, the damping ratio at 3 Hz will be close to 4%, and it is not possible to modify that without changing the damping ratios of the first two modes.
Mass damping will dampen out rigid body motions. For rotating blades for example, which undergo rigid body motions, this means that using
mass proportional damping will artificially dampen out the motion of the blades
, leading to lower power output than expected. For these cases, it is recommended not to use mass proportional damping. This is discussed in section 103 of
DNV-OS-F201 (2010)
.
Ashes offers different options to define your damping characteristics based on the input you have. These are defined by the
Structural damping mode
and the
Damping input
parameters in the Damping section of the
Analysis
tab in the
Analysis parameters
window.
1 Rayleigh damping defined by the structural characteristics
If you know the eigenfrequencies and the targeted damping ratios of your structure, you can input them so that Ashes solves the system of equations and determines the corresponding damping coefficients. This is obtained by setting the
Structural damping
mode
parameter to
Rayleigh
and the
Damping input
parameter to
Damping ratios
.
Note:
the mass and stiffness damping coefficients thus obtained can be found in the
Model Information
dialog
These coefficients should be positive. If the values entered for damping ration and period give negative coefficients, you will run into the Damping parameters give unphisical values warning
These coefficients should be positive. If the values entered for damping ration and period give negative coefficients, you will run into the Damping parameters give unphisical values warning
2 Rayleigh damping defined by the mass and stiffness damping coefficients
If you know the mass and stiffness damping coefficients, that is
$$\mu$$
and
$$\lambda$$
, you can input them directly into Ashes. This is obtained by setting the
Structural damping mode
parameter to
Rayleigh
and the
Damping input
parameter to
Explicit coefficient(s)
.
Note:
in this case, you can still input periods. These will
not
be used to compute the damping, i.e. they will not influence the simulation in any way. They are only used to show you relevant damping information in the
Model Information
dialog.
3 Stiffness proportional only
This mode can be used when the mass proportional part of rayleigh damping should be neglected. This can be obtained by setting the
Structural damping mode
parameter to
Stiffness proportional
, and is equivalent to having Rayleigh damping with the mass damping coefficient
$$\mu=0$$
. As for Rayleigh damping, it is possible to explicitely set the stiffness coefficient or to set the requested damping ratio at a given period.
Note:
in this case, you can still input a period. This will
not
be used to compute the damping, i.e. it will not infuence the simulation in any way. It is only used to show you relevant damping information in the
Model Information
dialog.
4 Mass proportional only
This mode can be used when the stiffness proportional part of rayleigh damping should be neglected. This can be obtained by setting the Structural damping mode parameter to Mass proportional , and is equivalent to having Rayleigh damping with the stiffness damping coefficient
$$\lambda=0$$
. As for Rayleigh damping, it is possible to explicitely set the mass coefficient or to set the requested damping ratio at a given period.
Note:
in this case, you can still input a period. This will
not
be used to compute the damping, i.e. it will not influence the simulation in any way. It is only used to show you relevant damping information in the
Model Information
dialog.