Docs > Theory Manual > Aerodynamics > Aerodynamic loads > DMST algorithm

DMST algorithm

The Double Multiple StreamTube (DMST) model is used to compute aerodynamic loads on the blades of a Vertical Axis Wind Turbine (VAWT). Similarly to the BEM algorithm, each blade is divided into a number of Blade aerodynamical stations, and the force exerted by the air on each station is computed. The DMST algorithm implemented here is based on the work of

Note: the DMST model is very similar to the Steady BEM algorithm. Some of the text and equations of this document are taken directly from the Steady BEM document.

The DMST model also uses the concept of induced velocity to calculate the aerodynamic loads on the blade elements: as a result of extracting kinetic energy from the flow, the velocity of the air is modified. This variation is represented by the so-called induced velocity. Estimating the induced velocity is key in determining the aerodynamic loads on the blade element.

The DMST algorithm makes an initial assumption on the value of the induced velocity for each streamtube. By means of blade element theory, this induced velocity is used to compute the lift and drag forces on a blade element. The conservation of momentum is then applied with these aerodynamic loads to calculate a new induced velocity. This new induced velocity is then compared to the initial assumption. If the two don't match within a certain margin, the new induced velocity is used as an input for the blade element theory and the process is repeated, until convergence is achieved

In the following we describe the algorithm applied on one blade element. The aerodynamic loads and induced velocities are computed within the Blade aerodynamical station plane. This plane, in which the Velocity triangle is shown, is perpendicular to the axis formed by the two nodes composing the blade element and lies at half the distance between the two. This implies that the Blade aerodynamical station plane follows the displacements of the blade element due to the elasticity of the blade. The follwing picture is drawn in the blade aerodynamical station plane:

We define the vectors x and y as unit vectors in the blade aerodynamical station plane such that y is in the rotational direction and x is perpendicular to y. In the present example, the blade station moves in the rotational direction, which produces a rotational velocity felt by the blade station in the opposite direction.

Notes:

The BEM theory uses the projection of the wind velocity in the blade station plane, which is here simply refered to as wind velocity.
The wind velocity is not in general perpendicular to the rotational velocity, i.e. it can have a component in the rotational velocity. For simplicity, in this section, any such component is added to the rotational velocity.

The steps followed in the steady BEM algorithm are listed and described below:

1 Initial estimation of the induced velocity

An initial guess is made on the induced velocity. The projection of the induced velocity in the x-direction, called axial induced velocity and noted Vi, is assumed to be 0.33 times the wind velocity:

it is common to define the axial induction factor a as

$$a=\frac{|V_i|}{|V|}$$

Note: the incoming wind considered in the DMST algorithm is different for the upstream and the downstream ahlves of the rotor. The assumption is that after passing through the upstream half of the rotor, the wind will have been slowed down by the presence of the VAWT. This is explained in more detail in section 9

2 Compute the angle of attack

At this stage, the induced velocity (noted W_i) is taken from the previous iteration. The angle of attack (noted

$$\alpha$$

) is the angle between the relative velocity and the chordline. The relative velocity (noted W) is the sum of the wind, rotational and induced velocities. The angle of attack is then obtained with the following equation

$$\alpha = \tan^{-1}\left(\frac{V(1-a)}{U}\right)-\beta-\theta$$

This is illustrated in the figure below

3 Look up the aerodynamic coefficients

Based on the angle of attack, the polars of the airfoil defined in the Airfoil polar file are looked up to obtain the lift, drag and moment coefficients

$$C_L, C_D$$

and

$$C_m$$

. If, for the considered airfoil, different polars are given at different Reynolds numbers, a local Reynolds number is computed following

$$Re = \frac{|W|\cdot C}{\nu}$$

where

$$C$$

is the chordlength (or the diameter for circular elements) and

$$\nu$$

is the kinematic viscosity of the air (set in the Atmosphere parameter). If the local Reynolds number thus calculated does not correspond to a Reynolds number for which a polar is given, the aerodynamic coefficients will be interpolated between the two closest polars. A linear or a logarithmic interpolation scheme can be chosen in the Aerodynamics tab of the Analysis parameters.

If the angle of attack does not correspond to a value given in the polars, a linear interpolation is performed between the two closest given values.

4 Compute aerodynamic forces

Once the aerodynamic coefficients have been established, the lift and drag forces are calculated with the following equations:

$$F_L=C_L\frac{1}{2}\rho|W|^2C$$

$$F_D=C_D\frac{1}{2}\rho|W|^2C$$

where

$$L$$

is the Influence length of the blade aerodynamical station and

$$\rho$$

is the density of the air (that can be changed in the Atmosphere parameter).

For a given blade aerodynamical station, the Influence length is defined as the distace between the middle point between the current blade station and the next blade station and the middle point between the current blade station and the next blade station, as illustrated in the image below

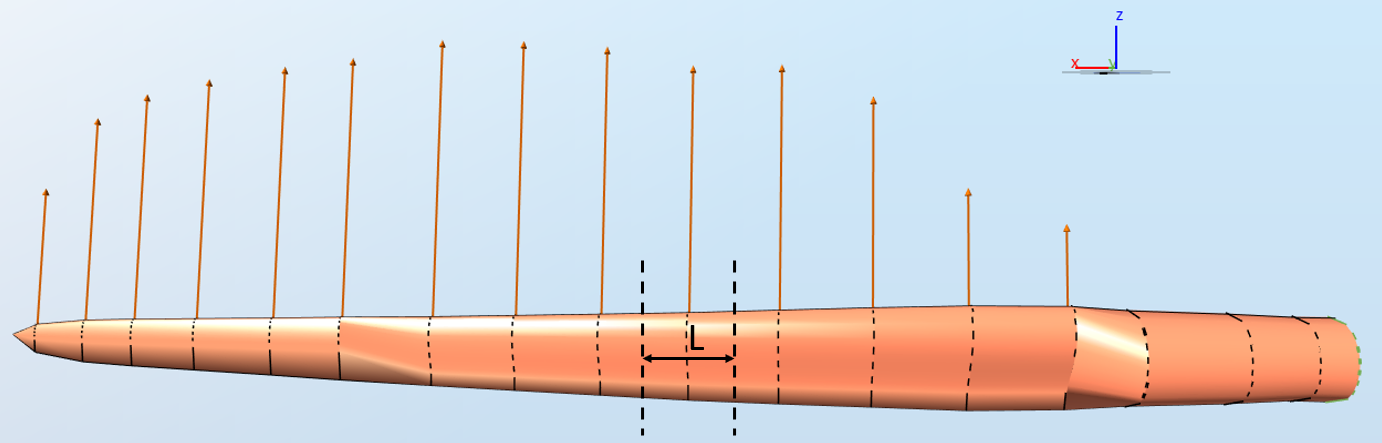
Note: no aerodynamic loads are calculated at the innermost blade aerodynamical station (at the blade root) or the outermost blade aerodynamical station (at the blade tip)

The drag force is applied in the direction of the relative velocity while the lift force is perpendicular to the drag force, as shown in the picture below

The locat thrust force

$$T$$

is then taken as the projection of the sum

$$F_D + F_L$$

in the wind direction.

The aerodynamic loads are applied at the aerodynamic center of the displaced blade aerodynamical section

5 Compute the induced velocity

From the local thrust force, an averag thrust force

$$T_{avg}$$

is computed as

$$T_{avg}=B\frac{\Delta\theta}{2\pi}T$$

where

$$B$$

is the number of blades and

$$\Delta\theta$$

is the azimuth angle variation during the considered time step.

A thrust coefficient

$$C_T$$

can ten be defined as

$$C_T=\frac{T_{avg}}{0.5\rho V^2\cdot A_{st}}$$

where

$$V$$

is the incoming wind speed and

$$A_{st}$$

is the area of the streamtube projected perpendicularly to the incoming wind. From this it can be deduced that

$$A_{st}=r\cdot\Delta\theta\cdot\sin(\theta)$$

, where

$$\theta$$

is the azimuth angle taken equal to 0 when the leading edge of the airfoil is pointing into the wind. Note that with this definition,

$$C_T$$

is not defined for

$$\theta=0$$

and

$$\theta = 180$$

. This case corresponds to the streamtube being infinitely thin, so the thrust will be 0 and thus the thrust coefficient will be 0 as well.

6 Compute the induced velocity

Once

$$C_T$$

has been obtained, the induction factor can be computed following the relation provided by momentum theory,

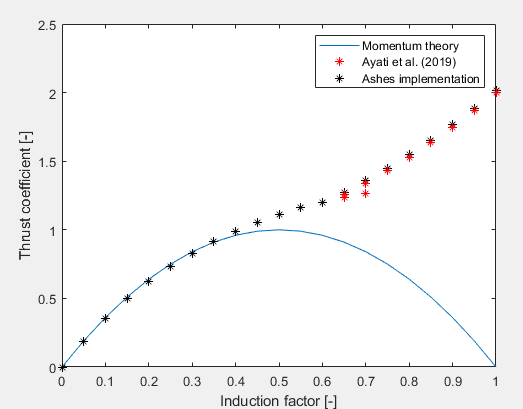
$$C_T=4a(1-a)$$

However, the momentum theory breaks down for heavily loaded rotors, that is values of the induction factor larger than 0.3-0.4. Therefore, a correciton needs to be applied, similar to the Glauert correction of the BEM method.

The correction implemented in Ashes is based on the work by Ayati. However, their results produce a discontiuity in the thrust coefficient curve around

$$a=0.7$$

that yields unphysical results, therefore a slight modification was implemented. The figure below illustrates the relationship between

$$C_T$$

and

$$a$$

for the different models. In Ashes,

$$a$$

is computed from

$$C_T$$

based o this curve.

7 Compare the induced velocity

Once the new induced velocity has been computed from the thrust coefficient, it is compared to the induced velocity obtained in the previous iteration. If the magnitude of the difference between the two is larger than 1e-8, the iteration is started again from step 2. Otherwise, the solution is considered converge

8 Compute the aerodynamic loads

Once the current induced velocity is calculated, the angle of attack is computed following step 2, the aerodynamic coefficients are looked up following step 3 and the aerodynamic loads are computed following step 4. In addition to the lift and drag forces, a pitching moment is calculated following the equation

$$M_p = \frac{1}{2}\rho W^2C^2L$$

The pitching moment is applied around the pitch axis

9 Incoming wind for the downstream half

The incoming wind speed is used hroughout this algorithm to compute first the lift and drag forces and then the thrust coefficient. As stated above, the wind speed considered for these computations will depend on whether the blade station is on the upstream half of the rotor or the downstream half.

If the blade station is on the upstream half, the incoming wind speed

$$V$$

is taken equal to the undisturbed wind speed

$$V_{\inf}$$

If the blade station is on the downwind half, the incoming wind speed

$$V$$

is taken as

$$V=(1-2a)V_{\inf}$$

, where

$$a$$

is the induction factor corresponding to the upstream part of the streamtube.

In the algorithm, every time an induction factor is computed in the upstream half of the rotor, it is stored together with its corresponding azimuth angle. When te algorithm is called for an azimuth angle in the downstream half, the corresponding induction factor is used to compute the incoming wind velocity. This happens all throughout the simulation, so the induction factors of the upstream half are constantly being updated depending on the wind conditions and rotational speed of the rotor.

Note: The induction factors of the upstream half are stored for the range of azimuth angles going from 0 to 180 in steps of 5. This means that the time step of the simulation should be small enough that the blade will not rotate more than 5 degrees in one time step. Otherwise, one risks the not to have any values of the upstream half stored for a particular azimuth angle, in which case the results for the downstream half will not contain the influence of the upstream half.

With this algorithm, a streamtube is divided into two parts: an upstream one and a downstream one. This is why the model is called Double multiple streamtube. If the streamtube is not divided into two, the model is simply called Multiple Streamtube, and the effect of the upstream half on the downstream one is not accounted for.