Tower shadow Powles model
This tests verifies that the implementation of the
Powles mode
for the tower shadow in Ashes corresponds to the description in . In order to verify the results, we compute the analytical solution for the aerodynamic loads that apply on the blades of a downwind ind turbine under different configurations that include the tower shadow.
1 Test description
The following load cases are tested:
- No tower shadow
- Tower shadow
- Tower shadow cd = 0.67
- Tower shadow azimuth = 5 deg
2 Model
This test uses the
Ondhore
template.
The csv to run this test can be downloaded from
here
.
The model used for this test is shown in the figure below. We acknowledge that it is not the prettiest wind turbine ever, but it serves the purpose of this test.

We use the blade from the
Cylindrical blade
test, which has a constant chordlength
$$c = 1\text{ m}$$
, and whose airfoils have a drag coefficient
$$C_D = 0.5$$
. The table below gives a summary of the relevant blade characteristics:
| Blade aerodynamical station | Distance to root | Influence length |
| 1 |
$$r_1 = 0$$
|
$$L_{I1}=1.25\text{ m}$$
|
| 2 |
$$r_2 = 2.5\text{ m}$$
|
$$L_{I2} = 2.5\text{ m}$$
|
| 3 |
$$r_3 = 5\text{ m}$$
|
$$L_{I3} = 1.25\text{ m}$$
|
The default tower has a constant diameter
$$a= 0.5\text{ m}$$
. The horizontal distance between the axis of the tower and the
Aerodynamical reference point
is
$$r = 3\text{ m}$$
and the hub radius is
$$h_r = 0.5\text{ m}$$
.
Gravity loads are not applied and the wind density is
$$\rho = 1.225\text{ kg}\cdot{m}^{-3}$$
. The rotor is fixed.
3 Analytical solution
For an incoming wind speed at the aerodynamical reference point
$$V$$
, the distributed drag force is given by
$$dF = \frac{1}{2}\rho c C_DV^2$$
The total force at the root of the blade is therefore
$$F = \Sigma_{i=1}^3dF\cdot L_{Ii}$$
The bending moment at the moment of the blade will be
$$M = \Sigma_{i=1}^3dF\cdot L_{Ii}\cdot r_i$$
To compute the effect of the tower on the incoming wind for a downwind wind turbine, Ashes uses the
Powles tower shadow model
. For this test, we compute the effect of the tower on a
Blade aerodynamical station
at a distance D of the center of the tower, as illustrated in the fogure below.
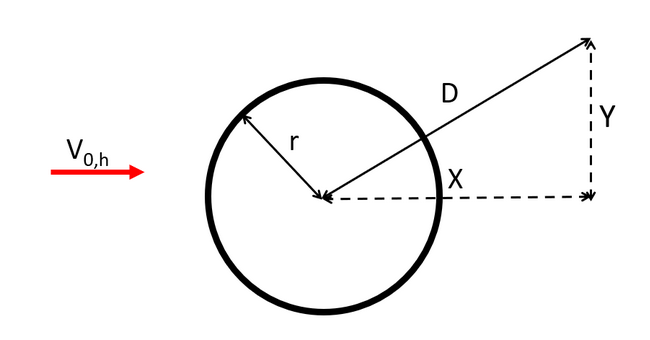
The wind velocity at the Blade aerodynamical station will be
$$V = V_{0,h}-u_{wake}V_{0,h}$$
, where
$$u_{wake}$$
is the
non-dimensional wake deficit
and is calculated according to the equations given in the
Powles tower shadow model
.
3.1 No tower shadow
If no tower shadow is applied, the incoming wind will be equal to the undisturbed wind,
$$V = V_{0,h}=10\text{ m}\cdot{s}^{-1}$$
.
In this case the
root force
will be
$$F = 153\text{ N}$$
and the
root bending moment
will be
$$M = 383\text{ Nm}$$
.
3.2 Tower shadow
For this load case, the tower and the blade are aligned, which implies that
$$D = 3\text{ m}$$
with
$$X = 3\text{ m}$$
and
$$Y = 0$$
. The drag coefficient of the tower is
$$C_{D,t}=1$$
This results in an incoming wind speed
$$V = 5.92\text{ m}\cdot{s}^{-1}$$
.
The
root force
will be
$$F = 53\text{ N}$$
and the
root bending moment
will be
$$M = 134\text{ Nm}$$
.
3.3 Tower shadow Cd = 0.67
For this load case, the drag coefficient of the tower is
$$C_{D,t}=0.67$$
. This results in an incoming wind speed
$$V = 7.26\text{ m}\cdot\text{s}^{-1}$$
The
root force
will be
$$F = 80\text{ N}$$
and the
root bending moment
will be
$$M = 202\text{ Nm}$$
.
3.4 Tower shadow azimuth 5 deg
For this load case, the blade is at an angle of
$$\theta = 5$$
degrees with respect to the vertical axis. This means that for each of the blade aerodynamical stations, the aerodynamical reference point will be at
$$X = 3\text{ m}$$
and
$$Y = \sin\theta\cdot(r_i+r_h)$$
from the centerline of the tower.
By computing the wake deficit for each blade aerodynamical station, we find that the wind veocities at the first, second and third stations will be
$$V_1 = 5.93\text{ m}\cdot{s}^{-1}$$
,
$$V_2 = 6.36\text{ m}\cdot{s}^{-1}$$
and
$$V_3 = 7.28\text{ m}\cdot{s}^{-1}$$
, respectively. This matches intuition, since the further along the blade, the further away from the tower and thus the less affected by the tower shadow a blade station is.
The
force root
will be
$$F = 65\text{ N}$$
and the
root bending moment
will be
$$M =179\text{ Nm}$$
4 Results
A simulation of five seconds is run. Since the analysis mode is
Loads only
, the output from Ashes is constant. The test is considered passed if the results from Ashes lie within 0.05% of the analytical solution.
The report for this test can be found on the following link: