In this document we compare results produced by Ashes to results published in the structural analysis book by Bell (1987b) .

The benchmark in Figure 6.6 from  Bell (1987b)  is used for this test, presented in the section below. For this benchmark, the simulation is run using the Linear  and Nonlinear  solvers (see Time domain simulation ) and modelling the beam with Euler-Bernoulli  beam theory or Timoshenko  beam theory. This will produce four sets of results.

In this example, an H-beam with length and supports as shown in the figure below is analysed.

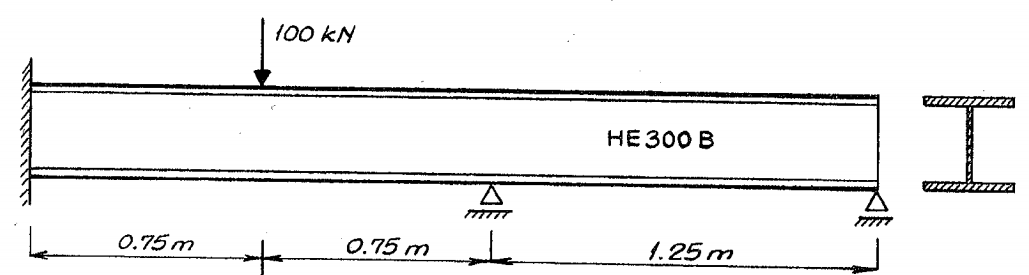
The shear area is given as   and the cross sectional area is   , which gives a shear correction factor  . The beam considered is an HE300B model, with an Elastic modulus  and a Poisson ratio  , which gives a shear modulus  .

Bell (1987b)  provides the displacement at the point of application of the load for two cases:

• without shear deformation (modelled with Euler-Bernoulli  beams in Ashes), the displacement is
  $$\delta=4.64\cdot10^{-5}\text{ m}$$
   

•   with shear deformation (modelled with Timoshenko  beams) is 
  $$\delta_T = 2.14\cdot10^{-4}\text{ m}$$
  .

Bell (1987b)  also provides the moment diagram for both cases, reproduced below:

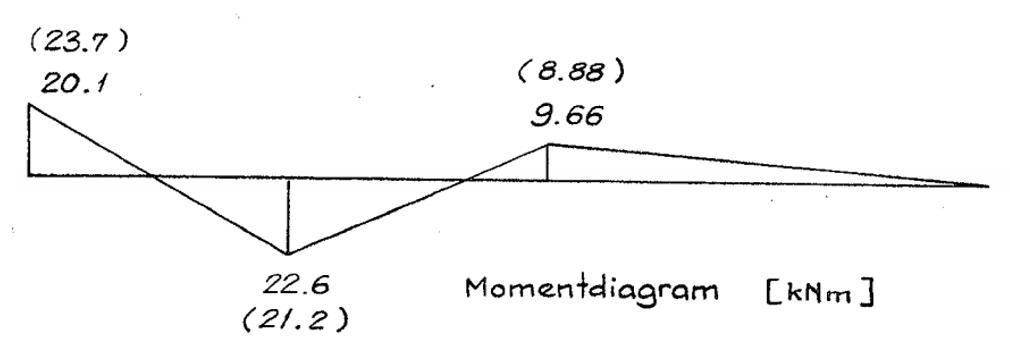
 In this figure, the values when considering shear deformation are given without brackets, and the values without shear deformation are in brackets.

The tests are run with the Linear and the Nonlinear  solvers.

The tests are run both with Rectangular shape and Circular shape  cross sections. For the circular shape cases, the beam is defined as having the same properties as the rectangular case in the deformation direction.

This produces a total of 8 load cases.

The test is considered passed when the last 20% of the Ashes time series lies within 1% of the benchmark value.

The report for this test can be found on the following link:

https://www.simis.io/downloads/open/benchmarks/current/Benchmark Bell.pdf